Деякі думки про точність вимірювань в електроприводі

"А якщо на велоколесо встановити енкодер буде ж краще ніж штатні датчики Холла? Енкодер точніший!" - такі питання мені інколи ставлять.

А насправді чи можна таким чином покращити точність вимірювання положення ротора безколекторного мотора і таким чином покращити керування електричним мотором? І взагалі, яка точність вимірювань потрібна, чи принаймні достатня, для датчиків положення ротора та датчиків вимірювання струму у системах керування безколекторними моторами? У це питання ми сьогодні будемо заглиблюватися. І мова буде не лише про векторне керування.

Про що ця стаття

У цій статті я не буду описувати як прикручувати енкодер до свого моторколеса, це буде доволі нудна і довга стаття про теорію. А кому кортить швиденько дізнатися чи буде зиск від конкретно цього енкодера (E38S6G5-600B-G24N) конкретно на моєму велоколесі (46 магнитів, 51 зуб, 500Wt) - НІ. Чому? тут вже треба розбиратися. Кому цікаво - читайте далі.

Я не знайшов літератури, статей, хоч якихось практичних рекомендацій з питань точності вимірювань у системах електроприводу. Тому запропоную свої думки та підхід. Якщо у когось є цікава інформація з цього приводу, будь ласка, поділіться у коментарях. Вам буду вдячний не тільки я, а і всі читачі цього блогу.

Нудна теорія

Інтуїтивно ми розуміємо, що чим точніший результат вимірювання, тим краще. І це безперечно так. Але цікавить два питання: "Яка мінімально точність вимірювань потрібна для керування електромотором?" Скажімо, ми беремо датчик струму і в документації читаємо: "Абсолютна точність 1.5%". Цього достатньо чи ні? І друге питання "З якого моменту підвищення точності вимірювання вже не має сенсу?" Тобто не буде давати помітного результату.

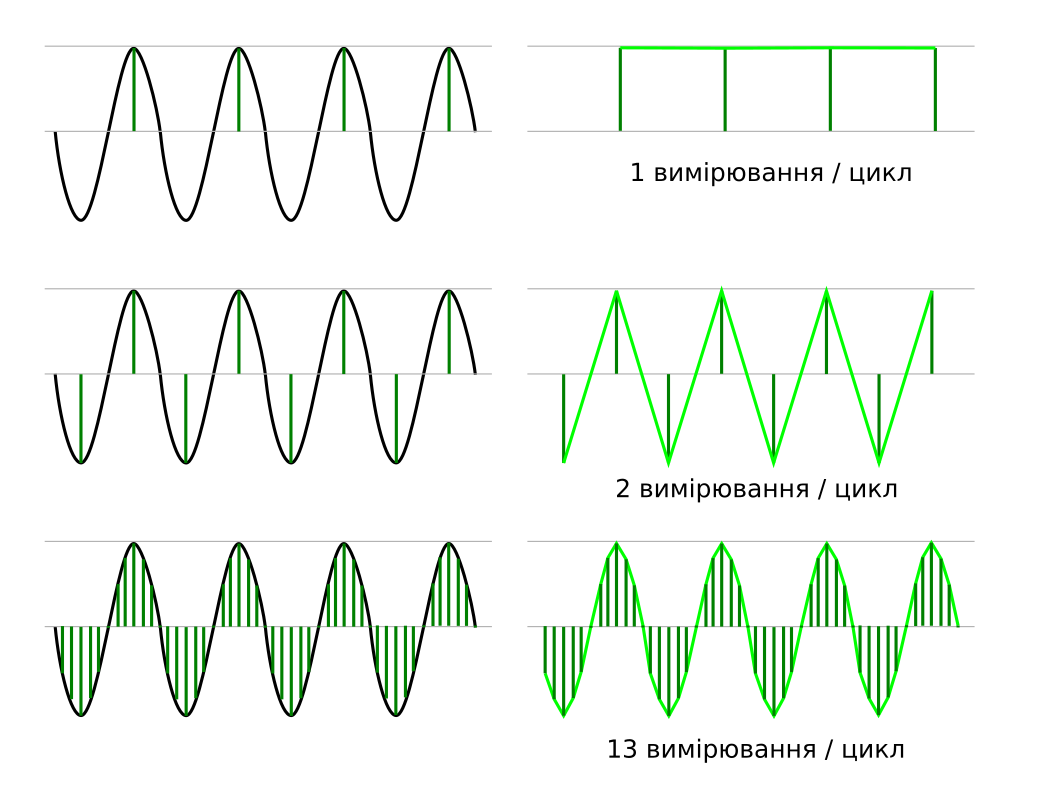
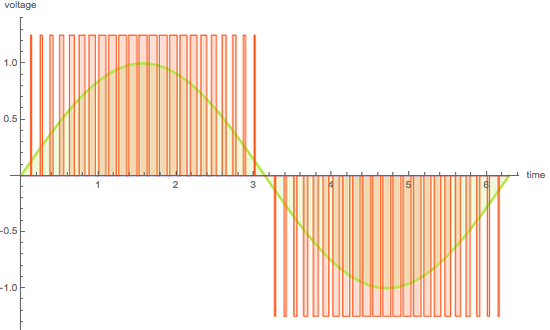
Отже, почнемо ми, як Ви любите, здалеку. А саме з усвідомлення того, що вимірювання будь-якого сигналу зі застосуванням мікроконтролера квантовано у часі, тобто має певну періодичність. А між вимірами проходить певний час і що коїться з сигналом у цей проміжок часу ми не знаємо напевно і вважаємо, що сигнал не змінюється. Якщо ми вимірюємо сигнал, який змінюється у часі з якоюсь частотою, очевидно, що частота вибірки, тобто частота вимірювання має бути більшою за максимально можливу частоту сигналу. Щоб не проґавити момент, коли сигнал змінився. А мінімальна частота цієї вибірки має бути більшою ніж подвоєна максимальна частота сигналу. Це правило не я придумав (шукай/читай: Теорема Найквіста—Шеннона—Котельнікова). Звісно, з мінімально допустимою частотою вибірки ми не зможемо досконало представити форму сигналу, але це мінімальна частота яка дозволяє хоча б оцінити що відбувається з сигналом. При менших частотах не буде навіть шансу відслідити періодичність сигналу.

Зрозуміліше стає, коли це представити у графічній формі.

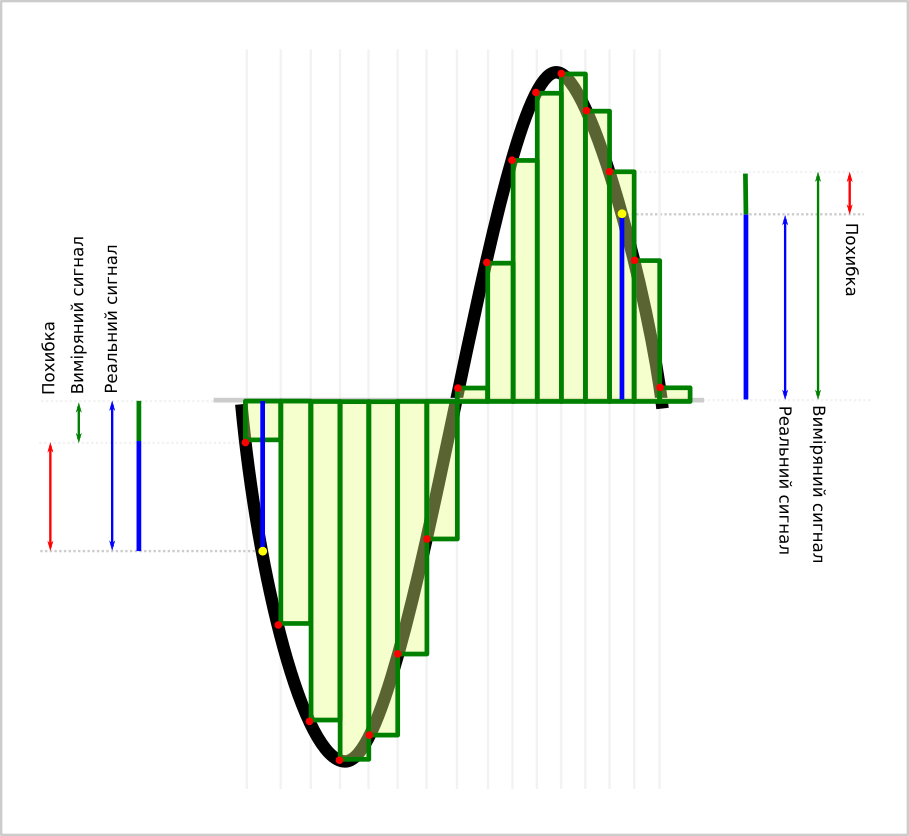
Очевидно, чим вища частота вибірки, тим більш близький результат форми ПРЕДСТАВЛЕНОГО сигналу до форми реального сигналу. І таким чином ми можемо сказати, що частота вибірки якось та й впливає на похибку. Чим вища частота, тим менше викривлення у ПРЕДСТАВЛЕННІ виміряного сигналу. При чому принципово зрозуміти, що мова йде не про похибку кожного конкретного вимірювання, кожне окреме вимірювання може бути взагалі без похибки (абсолютно точним), як на графіках, а мова йде про похибку, у представленні виміряного сигналу, яка з'являється саме через те, що сигнал вимірюються через проміжки часу. І ця похибка у стратегічному плані впливає на керування системою. Тобто, ми можемо абсолютно точно вимірювати сигнал, але не дуже часто та отримати викривлену картину. В результаті система керування не зможе правильно оцінювати що коїться і не зможе ВЧАСНО приймати правильні рішення. А так "все чотко" - датчики мають абсолютну точність.

Наприклад, у період між вимірами сигналу можемо отримати досить велику похибку через те, що сигнал вже змінився, а система про це ще не знає і не може вчасно відреагувати.

"Дядьку, та шо ти тут чешиш?" - Скаже дехто. Типу - "... ми виміряли сигнал от зараз, обрахували та задали керуючий сигнал. Всьо! Де проблема? Ну так же ж?". Ага, але є нюанс.

Виникають деякі питання з часом прийняття рішення. Якщо вимірювання сигналу потребує деякий час, потім прийняття рішення (в нашому випадку якийсь обрахунок мікроконтролером) потребує деякий час, потім передача керуючого сигналу потребує час, і виявляється, що система видає дію з запізненням, коли реальний вхідний сигнал вже змінився. Тобто з'являється похибка керування, викликана часом, який потрібен для вимірювання і прийняття рішення системою. І виникає питання: "а може нам і не потрібно абсолютно точно вимірювати сигнал коли через запізнення ми все одно не зможемо точно попасти куди треба?" Якщо зробити так, щоб ці похибки (похибки вимірювання і похибки керування) не складалися, тоді нам достатньо, щоб похибка вимірювання сигналу була не більшою за похибку керування.

Трішки заплутано, але сподіваюсь далі стане ясніше.

Вплив PWM

Отже, у системах керування електромоторами всі вимірювання і зміна напруги на фазах мотора теж виконуються періодично. Частота цих вимірювань залежить від частоти PWM. Тобто, вимірювання струмів у обмотках статора, визначення положення ротора, обчислення вектора напруги - все це відбувається синхронно з частотою PWM. Це ми говоримо про векторне керування.

Чому не частіше? Тому що ми не можемо змінювати PWM частіше ніж частота самого PWM. Тобто, якщо у поточному періоді PWM ми задаємо новуі параметри, шпаруватість PWM, то вони застосовуються на зараз, а коли почнеться новий період PWM. Через це і виникає деяка затримка керуючого сигналу. І якщо ми до початку нового періоду PWM встигнемо обрахувати та задати йому декілька значень, то це дурна робота, бо застосовано буде лише останнє задане значення. І весь наступний період PWM ми знов не зможемо змінити його шпаруватість.

От і виходить що змінювати параметри PWM (а відповідно і вектор напруги) ми можемо не частіше ніж частота PWM. Відповідно, вимірювати сигнали та вираховувати значення PWM частіше ніж його власна частота не має сенсу. Отже, частота вимірювання сигналів дорівнює частоті PWM. Очевидно, що збільшивши частоту PWM, ми зможемо скоротити період вимірювань і обчислень і точніше керувати мотором (теоретично).

З технічних причин ми не можемо збільшувати частоту PWM до будь-яких значень. Вона лімітована особливостями роботи силових ключів.

Отже, маємо констатувати, що виміри струму і положення ротора відбуваються з частотою PWM. Зміна параметрів PWM, тобто напруги на фазах двигуна, можна сказати, вектора напруги, відбувається теж не частіше ніж частота PWM.

Але ж це досить часто! Затримки маненькі! Хіба це впливає на результат? А порахуймо!

Цікаві розрахунки

Далі застосовується ряд спрощень і припущень. Будемо вважати, що:

• Математичні операції не вносять суттєвої похибки.
  Після виміру струму і положення ротора результатом обчислень буде вектор напруги, і далі розподіл напруги по фазах двигуна. Припускаємо, що математичні операції, які це виконують, не вносять суттєвої похибки.
• Похибку від квантування у часі можна прийняти за ОЦІНЮВАЛЬНЕ значення для похибки датчиків.
  Це грубувато, але достатньо для оцінки необхідної точності датчиків. Тобто, у своїх судженнях я допускаю, що якщо похибка, що спричинена квантуванням становить +-1%, то і похибка датчика +-1% цілком допустима і суттєво не вплине на результат. Хоча, так, формально похибки мають складатися, але якщо поглянути на інфографіку, можна помітити, що в деяких випадках похибка від квантування може бути значно помітнішою. Тому, хоча це припущення і може викликати критику, ми будемо вважати що якщо похибка датчика не більша за похибку від квантування, то такої точності датчика буде достатньою. Завдяки цьому припущенню ми зможемо хоча б приблизно визначити необхідну точність датчиків. Тобто основна ідея така, якщо ми можемо керувати з точністю +- якийсь відсоток, то і датчиків с такою ж похибкою буде достатньо.

Зараз буде зрозуміліше. Вйо до цифірок!

Приклад #1

Уявімо, що ми маємо двигун з 4-полюсним ротором, вал якого здатен обертатися з максимальною швидкістю 3000 об/хв.

3000 об/хв. 2 пар полюсів

3000*2 = 6000 об/хв. ел. поля статора. Це 6000 / 60 = 100 об/сек. ел. поля статора.

При частоті ШІМ 16000 Гц ми зможемо виміряти струм/положення ротора 16000 / 100 = 160 разів за один повний оберт магнітного поля статора.

Тобто між кожними вимірами (Піком ШІМ) ротор буде встигати обертатися на 360/160=2,25 градуса. А магнітне поле статора за цей час буде (умовно) не змінним через особливості роботи PWM про які я вже казав.

2,25 градуса - це 0,625% від 360 градусів.

Отже, при таких умовах ми зможемо встановлювати вектор напруги з кроком, або назвемо це теоретичною точністю керування 0,625%. І при таких умовах виконувати вимірювання з більшою точністю вже не має сенсу. Точності у 0,625% буде умовно достатньо.

Приклад #2

Але при зниженні обертів, скажімо, до 300 об/хв. маємо наступні результати:

300 об/хв. 2 пар полюсів

300*2 = 600 об/хв. ел. поля статора. Це 600/60 = 10 об/сек. ел. поля статора.

При частоті ШІМ 16000 Гц ми зможемо виміряти струм/положення 16000 / 10 = 1600 разів за один повний оберт магнітного поля статора.

Тобто між кожними вимірами (Піком ШІМ) ротор буде встигати обертатися на 0,225 градуса.

0,225 градуса - це 0,0625% від 360 градусів.

Тобто, на менших обертах підвищення точності вимірювань вже має сенс. Але знайдіть ще датчики з точністю 0,0625%. Але то вже більш практичне питання, яке дзеркально поставить інше питання - чи варто намагатися точніше керувати мотором коли датчики не "альо"? Та з цим розберімося пізніше.

Приклад #3

Велоколесо робить 430 об/хв. (52 км/год.) 46 магнітів = 23 пар полюсів

430 * 23 = 9890 об/хв. ел. поля статора. Це 9890 / 60 = 164,833 об/сек. ел. поля статора.

При частоті ШІМ 16000 Гц ми зможемо виміряти струм/положення 16000 / 164,833 = 97,067745197 разів за один повний оберт магнітного поля ротора.

Тобто між кожними вимірами (Піком ШІМ) магнітне поле статора буде встигати обертатися на 3,70875 градуси.

3,70875 градуси - це 1,030% від 360 градусів.

Висновки

Ми змогли відповісти на перше запитання про мінімальну необхідну точність. Ми з'ясували яка теоретична точність потрібна - для наших прикладів - не гірше 0,625% та 1,03% відповідно. Звісно, це приблизні теоретичні цифри, але вже щось є, від чого можна відштовхуватись.

Думаю Ви звернули увагу на те, як змінюється необхідна точність залежно від швидкості обертання вала мотора. Чим повільніше вал мотора обертається (перепрошую, не вал, а магнітне поле статора, так буде точніше), тим менше вплив частоти ШІМ на похибку керування і тим логічніше використовувати більш точні датчики.

Точність датчиків положення статора (теоретична)

Рухаємось далі у напрямок питання про енкодер.

ОК, ми з'ясували яка нам точність потрібна. Ну хоча б орієнтовно. А от цікаве питання: "яку ТЕОРЕТИЧНУ точність вимірювання забезпечують датчики положення ротора?"

Три дискретних датчики Холла

Як вираховується положення ротора завдяки трьом дискретним датчикам Холла і таймера мікроконтролера?

Чітко визначити положення ротора можна лише у моменти перемикання датчиків. Всього таких положень 6 за один повний оберт магнітного поля ротора. Щоб визначити положення ротора у будь-який момент застосовують таймер. Вимірюється час, за який ротор обернувся від одного спрацювання датчиків до наступного. Тепер у будь-який момент можна вирахувати положення ротора, допускаючи, що швидкість обертання ротора зміниться не суттєво.

Таймер, який вимірює цей час, працює на з певною частотою і це теж вливає на точність.

Наприклад, для мого велоколеса:

Якщо таймер, що обслуговує датчики Холла, працює на частоті 1Mhz, буде 1000000 / 164,833 об/сек. ел. поля статора = 6066 тактів на оберт. Це один такт на 0,059347181 градуса. Це при максимальних обертах мого велоколеса. 0,059347181 градуса - це 0,016485328% від 360 градусів. Тобто, теоретична похибка цього метода вимірювання положення ротора близько 0,01%!?

Так, але ця теоретична точність на практиці ілюзорна і не досяжна бо - датчики різні за характеристиками через допуски у виробництві, криво встановлені, магніти ротора різні, вал б'є, зазор плаває, все це впливає на реальну, фізичну точність, яка в реальності на жаль значно, значно гірша. Але поки що про теорію.

Eнкодер

Тепер уявімо, що нам вдалося встановити енкодер на велосипедний мотор-колесо.

Як вираховується положення за допомогою інкрементного енкодера? Точність цього датчика не залежить від швидкості обертання. Тобто розглянуті далі датчики працюють з точністю яка НЕ залежить від швидкості обертання і PWM, лише від характеристик самого датчика і кількості пар полюсів двигуна. Бо осьові датчики встановлені на валу мотора і не відстежувати магнітне поле ротора, а нам потрібно знати положення магнітного поля ротора.

Енкодер квадратурний інкрементний E38S6G5-600B-G24N

Енкодер - 600 тактів на оберт. - Оберт механічний. Тобто, на один електричний оберт кількість тактів енкодера буде 600 / кількість пар полюсів. На моєму моторі колесі 23 пари полюсів. 600 / 23 = 26,087 тактів на один повний електричний оберт. Виходить один такт на 13,8 градуса. 13,8 градуса - це 3,833% від 360 градусів.

Ця точність значно гірша за точність метода з дискретними датчиками Холла. Отже, цей не дешевий інкрементний енкодер буде гіршим за датчики Холла у випадку з моїм мотор-колесом.

Абсолютний магнітний енкодер MT6701

Incremental ABZ Resolution 1~1024 Pulses per Revolution (PPR) User Programmable

1024 / 23 = 44,52173913 один такт на 8,0859375 градусів. 8,0859375 градусів - це 2,24609375% від 360 градусів.

Ця точність теж значно гірша за точність метода з дискретними датчиками Холла.

Абсолютний магнітний енкодер AS5600

AS5600 12-bit analog

4096 / 23 = 178,086956522 один такт на 2,021484375 градусів. 2,022 градусів - це 0,562% від 360 градусів.

Краще, але теж не найкращий результат (теоретичний результат).

Коли енкодер - це добре?

Але ж енкодери використовують, може тут якась помилка?

Енкодери використовують (але не скрізь) і вони дійсно кращі, але при певних умовах. По-перше, оскільки енкодери мають характеристику типу Pulses на фізичний оберт, логічно їх застосовувати на моторах з малим числом пар полюсів. Енкодери вкрай корисні, коли вал мотора обертається дуже повільно, або у режимах стабілізації положення, коли вал мотора з дуже невеличкою швидкістю рухається в одному та іншому напрямку. В цих ситуаціях метод визначення положення ротора з дискретними датчиками Холла вже не працює, бо вал майже не обертається і точно визначити положення вкрай складно. І тут енкодери мають шалену перевагу. Навіть енкодери з посередньою точністю. А от на великих стабільних обертах, від енкодера мало користі. Я маю на у вазі масштаби вело колеса.

І для багатополюсного мотора осьовий енкодер може бути не дуже гарним рішенням.

Тому саме такі енкодери на моєму велоколесі у режимі звичайної їзди помітного результату не дадуть. А при блочній комутації, коли вектор напруг скаче кроками по 60 градусів - взагалі ні про що і говорити.

Про точність на прикладі секторів

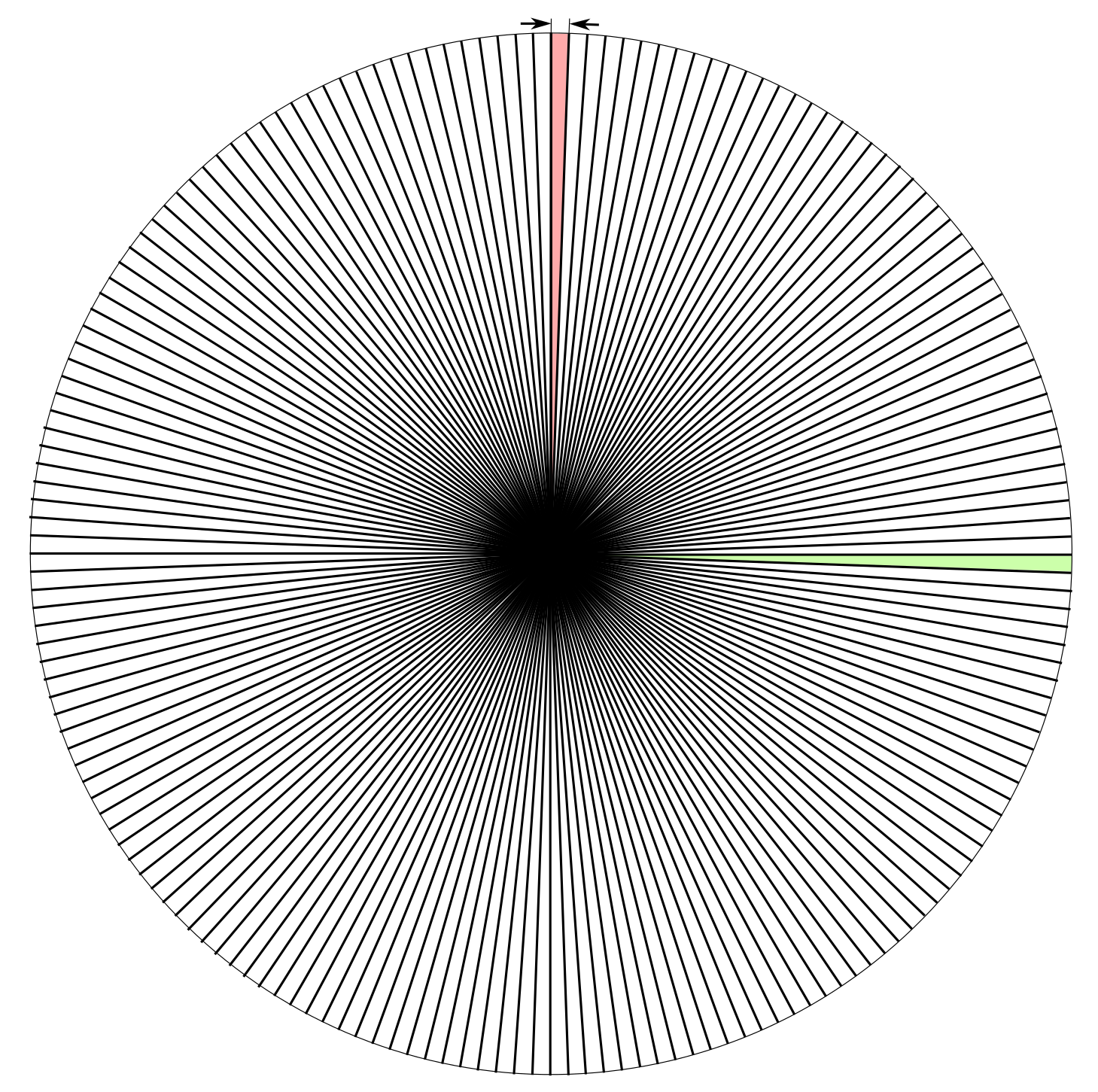
Повернімося до роздумів про точність. Уявімо коло по якому обертається ротор мотора, вектор струму, напруги, і це коло розбито на умовні сектори.

Уявіть що датчики струму має обмежену точність яка гарантує, що вирахований вектор струму гарантовано попаде в якийсь сектор (на малюнку позначений червоним). Розмір сектора - це похибка датчиків струму. А датчик положення ротора у нас абсолютно точний, з нульовою похибкою. Тоді, коли ми вирахуємо вектор напруги абсолютно точно, ми все одно отримаємо на виході похибку розміром у такий же сектор (на малюнку позначений зеленим). Виходить, що і встановлювати вектор напруги з абсолютною точністю не має сенсу, головне, щоб він попав у сектор такого ж розміру.

А якщо у нас датчик положення ротора буде мати похибку, яка гарантує попадання у такий самий сектор, цього буде достатньо. Нічого помітно не погіршиться. Якщо покращувати точність якогось одного датчика, це помітно не покращить загальну точність керування мотором. Лише комплексне покращення дасть результат. Коли датчики струму будуть попадати у менший сектор, і датчик положення ротора буде попадати у менший сектор, і система що формує вектор напруги (з усіма приколами PWM) зможе забезпечити встановлення вектора напруги з такою ж точністю, тоді результат покращення буде помітно.

Коротко кажучи, покращувати треба все в комплексі, чи хоча б починати з най НЕ точнішої ланки.

І тут існує ще взаємний зв'язок. Коли ми з'ясували що датчики мають якусь певну точність, ми можемо не намагатися керувати мотором точніше (підвищувати частоту PWM, вдосконалювати математику тощо) бо наявні датчики все одно не дадуть нам точніше керувати мотором. І навпаки, коли маємо обмеження по точності керування мотором, ми не намагаємось використовувати датчики, які набагато точніше. Інакше ефекту не буде.

На жаль не лише датчики впливають на "неточності". Треба враховувати якість виготовлення двигуна. Якщо він кривий, зазор плаває, магніти вже перегрівалися або різні з народження, якщо пластини статора трохи розійшлися, обмотка в пазах зсувається, його більш точнішими датчиками спасати скоріш за все не вийде.

Все, що я вище виклав, здебільшого стосується векторного керування і синуса, у BLDC з його блочною комутацією взагалі біда, бо вектор напруги скаче кроками по 60 градусів (а це 16.6% від повного кола). Якщо у Вас точність датчика положення ротора була +-2%, а ви її покращили вдвічі, тобто до 1%, сенсу з того буде не багато, бо все одно крок вектора напруги - ще 16.6% . На цьому тлі покращення звісно якесь може і буде, але не так помітно, якби ви вдвічі покращили точність встановлення вектора напруги. Або перейшли на синус.

А ви молодець! Дочитали до кінця! Я Вам ставлю "лайк"!

Звісно, це лише мої думки, але я їх теж вирішив перевірити на практиці у своїй реалізації векторного керування. То ж коли у майбутньому Ви побачите мій програмний код, і згадаєте цю статтю, буде простіше розібратися чого там так все реалізовано.

У своїй реалізації векторного керування я насправді оперую не градусами чи радіанами, бо обчислення у мене в полярних координатах, а оперую номерами секторів. Так, це ціле число, з ним дуже просто працювати - економить ресурси мікроконтролера. А розмір сектора обертається меншим за похибку най не точнішого датчика. Звісно, за потреби, розмір секторів можна зменшити.

На цьому поки що все. Сподіваюсь, що Ви не задрімали. Бажаю успіхів.

P.S. Розумію, що зміст статті може викликати непорозуміння через нашу звичку сприймати навколишні процеси я щось неперервне. Але прошу, враховуйте що зі сторони мікроконтролера світ виглядає як набір семплів.